March 14 is celebrated by nerds around the world as the Pi Day. When written in digits, 3/14 represents first three digits of the number traditionally represented by the Greek letter “π” (pronounced pi) – 3.14. Pi Day is celebrated by eating pie and discussing the significance of π. Some folks who have too much time on their hands compete at memorizing decimal digits representing the value of pi. The record presently stands at 67,890 digits! While eating pie is optional, discussing the significance of π is truly mandatory.
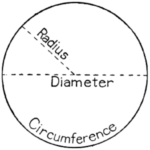
So, what is π and why is to so important? π is arguably the most famous mathematical constant, expressing the ratio between the circumference of a circle and its diameter. If you take a circle with a diameter of 1, the circumference of this circle will measure approximately 3.14159265… —“approximately” being the operative word here, but more on that later. Thus, for a circle of radius (half of the diameter) “r”, the circumference of the circle measures 2πr, and the area of the circle is calculated as πr2. One can see why π is so important in measuring land, for instance.
However, π appears not only in geometry, but in number theory, algebra, analysis, statistics, and other mathematical disciplines. In physics, π is truly ubiquitous.
In antiquity, Babylonians approximated π as the closest whole number – 3. However, measuring land, architecture, and engineering all require knowledge of π with reasonable precision. The Babylonians knew that the integer 3 was merely a rough approximation.

Babylonian tablet
A Babylonian tablet found near Susa (c. 19-17 centuries BCE) gives an approximation of π as 25⁄8 = 3.125, getting the first decimal right.

Rhind Papyrus
The Egyptian Rhind Papyrus (c. 1600 BCE) approximates π as 256⁄81 ≈ 3.16. Some Egyptologists claim that the builders of the pyramids used the ratio 22⁄7 = 3.142… for π. Of course, the first two decimals in this approximation are correct. In the Shatapatha Brahmana (c. 6th century BCE), Indian astronomers estimated π to be 339/108 = 3.139…

Archimedes of Syracuse
In the 3rd century BCE, Archimedes proved that π is greater than 223⁄71 ≈ 3.1408…, but less than 22⁄7 ≈ 3.1428… In the 2nd century BCE, Greek astronomer Ptolemy used an approximation of 377⁄120 ≈ 3.1416… In the 3rd c. CE, The Chinese mathematician Liu Hui very accurately approximated π to four decimals as 3927/1250 = 3.1416. In the 6th c CE, Indian mathematicians obtained the same value of π as 62832/20000 = 3.1416. By the 5th century CE, Chinese mathematicians improved the value of π till the seventh digit. Today, the value of π is known to trillions of digits.

Gottfried Leibniz
The exact value of π was first discovered by German mathematician Gottfried Leibniz. Leibnitz’s formula for π is an infinite series:
The fact that the exact value of π can only be expressed as an infinite series is highly significant, as we will see later.
The Jews who left Egypt must have been aware of the approximate value of π then used by the Egyptians – after all, Jewish slaves built the Pyramids. Thus, some raise a question, why the Tanakh gives the crudest approximation of π. Indeed, in I Kings 7:23 we read:
Then he made the molten sea of ten cubits from brim to brim, round in compass, and the height thereof was five cubits; and a line of thirty cubits did compass it round about.
Similarly, in II Chronicles 4:2 we find an almost identical passage:
Also, he made the molten sea of ten cubits from brim to brim, round in compass, and the height thereof was five cubits; and a line of thirty cubits did compass it round about.

The round basin made out of cast metal for the Beit HaMikdash (First Temple) in Jerusalem by King Solomon had a diameter of 10 cubits and a circumference of 30 cubits. Accordingly, it seems that π is implied to be 3. The First Temple was built by King Solomon in 832 BCE. By that time, the Babylonians and Egyptians already knew better than that.
Even if we were to assume, arguendo, that the ancient Hebrews did not know the value of π beyond its integer value (3), they certainly knew how to measure. If they made the basin with a diameter of 10 cubits, when they measured its circumference, they would find it to be approximately 31.41 cubits; rounding to the nearest integer would result in 31 cubits, not 30. The Lubavitcher Rebbe, Rabbi Menachem Mendel Schneerson, explained this as follows: The circumference of the basin was actually 30 cubits. Accordingly, the diameter was approximately 9.55 cubits and was rounded up to the integer 10. This explanation resolves the question of why the circumference was 30 cubits and not 31.
In reality, I don’t see a problem here at all. The Tanakh is not a textbook on mathematics. Nowhere in the quoted verses the prophets set out to reveal to use the value of π. The verses describe the dimensions of the basin used in the Temple. As the Rebbe explained, given the circumference of the basin at 30 cubits, the diameter came to be a shade under 10 cubit and was simply rounded off to 10. The basin was already built, so there was no need for precise engineering drawings or exact dimensions. The Scripture simply informs us of approximate dimensions of the basin, which are rounded off to integer numbers. There is nothing strange or unusual about it.
However, some of our sages thought that the verses cited above required an explanation. Thus, Mishnat ha-Middot seeks to solve this problem by positing a brim approximately 0.225 cubits thick, which was included in the measurement of the diameter, but not in the circumference. Thus, it approximates π to be 22⁄7, or 3.14135… The dating of this source, however, is unclear. Some attribute it to the Tana, Rabbi Nechemiah, in which case this work can be dated to c. 150 CE, while other authorities date this book to the late Gaonic period, c. 9th century CE.
Fast forward to the twentieth century, and Rabbi Max Munk offered interesting insight on the verses in Tanach. (This insight is often misattributed to the Vilna Gaon. This was strongly disputed by Prof. Elishakoff and Dr. Pines in the article “Do Scripture and Mathematics Disagree on the Number π?” B’Or HaTorah, 17, pp 141-42.)
In I Kings, the written word (ktiv) used for “diameter” is “קוה” (Kuf-Vav-Heh), which makes no sense in this context. By contrast, in Chronicles II, the word for diameter is spelled as “קָו” (Kuf-Vav), meaning “line.” However, according to the Mesorah (Masoretic tradition), the word in I Kings is read differently than it is written (kri)—it is read as קָו (Kuf-Vav), just as it is written in Chronicles II. Rabbi Munk points out that the gematria of קוה (100+6+5) is 111 and the gematria of קו (100+6) is 106. He interpreted the ratio of these two values – 111/106 – as a correction factor: if you multiply the implied value for π (3) by this factor, you get 333/106 = 3.14150…– an approximation of π accurate to the fourth decimal point. This would be a far more accurate approximation of π than was known for many centuries thereafter.
Ultimately, no matter what ratio you find, it will always be just an approximation of the true value of π and therefore will always be open to criticism.

Maimonides
The real problem is that π can never be truly expressed as a ratio of two integers – it is an irrational number (rational numbers are those that can be expressed as a ratio of two integers). Interestingly, it was Maimonides (the Rambam) who was the first to assert that π is irrational. In explaining a Mishna that posits 3 as the halachic (legal) value of π, Maimonides explains that the number 3 is as good an approximation as any other, because we cannot compute π precisely anyway. Besides being an irrational number, π is also a transcendental number, meaning that it is not a solution or a root of an algebraic equation.

Leopold Kronecker
I once asked Rabbi Adin Steinzaltz (may he have refuah shaleimah), if irrational and transcendental numbers are real, where can we find them in the Torah?” In response, Rabbi Steinzaltz quoted a famous statement by the 19th century Jewish-German mathematician Leopold Kronecker, who said: “Die ganzen Zahlen hat der liebe G-tt gemacht, alles andere ist Menschenwerk” (G-d made the integers, all else is the work of man).
This is no trivial question. In fact, it is the crux of the debate in the philosophy of mathematics whether mathematical objects “exist” in some ontological sense and are being “discovered” by mathematicians, or they are “invented” by mathematicians and exist only in our minds. Plato founded the school of thought that mathematical objects exist as ideal forms and are discovered by us. Kronecker, on the other hand, espoused the opposite view. It seems to me that, by choosing an integer number (3) that is a poor approximation of π, the Prophets were not demonstrating ignorance of better approximations well known in antiquity; rather, they were revealing to us something else – a deep truth about the nature of mathematics. As Kronecker expressed it, “G‑d made the integers, all else is the work of man.”
Georg Cantor
As Georg Kantor proved in the 19th century, there are infinitely more irrational and transcendental numbers than rational numbers. Moreover, rational and irrational numbers represent two different kinds of infinity. Integer (and rational) numbers can potentially be counted ad infinitum, but at any given point in time, there are always a finite number of them that you’ve counted so far. Rational numbers are said to be countable. This type of infinity is called a potential infinity. Real numbers that include irrational and transcendental numbers are different. If you take a real line and mark a finite segment on it, say between zero and one, there will be an infinite number of points (i.e., real numbers) on this segment. Irrational numbers are said to be uncountable. Such infinity is called the actual infinity.
The Midrash Rabba says that when creating the world, G-d looked into the Torah as into blueprint. None of these numbers are to be found in the Torah. No amount of gematria calculation can lead to an irrational or a transcendental number, such as π. If they are real, why aren’t we finding them in the Torah – the blueprint of the creation? Or, perhaps, the Torah tells us they are not there because they are not real (no pun intended)?

Ernst Mach
The question of the use of real (let alone complex) numbers that include the irrational and transcendental number in physics is highly questionable. Ernst Mach (a philosopher of physics of the Mach Principle fame who profoundly influenced Einstein), as other positivist philosophers, felt that only physically measurable quantities ought to be allowed in a physical theory. However, whenever we measure something, the result is always an integer number or a rational number, never irrational or transcendental. How then are we allowed to use irrational and transcendental numbers in physics, if they are not countable? I’ve struggled with this question since I was a teenager. I never found an answer… Perhaps, we need to build for physics special mathematics based on rational numbers only? This is one of many questions and mysteries of the number π.
###
(The abridged version of this article was published today by The Jewish Press)



Can you give the Source Page and Safer for Rabbi Munk 111/106 ratio? Many people are apparently attributing this incorrectly to the Gaon of Vilna.
I would love to get the source correct.
See “Do Scripture and Mathematics Disagree on the Number π?” by Prof. Elishakoff and Dr. Pines in the article in B’Or HaTorah, 17, pp. 141-42
The original sources are:
Rabbi Max Munk, 1962: Three Geometry Problems in Tanach and Talmud (in Hebrew), SINAI (Mossad Harav Kook) 51 (5722) 218-227.
Rabbi Max Munk, Rabbi 1968: The Halachik Way for the Solution of Special Geometry Problems (in Hebrew), HADAROM (Rabbinical Council of America) 27 (5728) 115-133.
“Fast forward to the twentieth century, and Rabbi Max Munk offered interesting insight on the verses in Tanach. (This insight is often misattributed to the Vilna Gaon. This was strongly disputed by Prof. Elishakoff and Dr. Pines in the article…”
Could you clarify? What was strongly disputed by Elishakoff and Pines? That the gematria is true? Or just that the Vilna Gaon said it?
Prof. Elishakoff and Dr. Pines disputed that the Vilna Gaon said it. The gematria is correct–you can check it yourself.