The Special Theory of Relativity, published by Albert Einstein in 1905, was a game changer. It ushered the era of new physics dubbed by some as the “Jewish physics.” And Jewish physics it was.
At the core of Special Relativity is the notion of the relativity of motion – all motion is not absolute, as Newton thought, but is relative to something else, to a particular point of view. In physics, we define a point of view as a frame of reference. If you are standing in a moving train, leaving the railroad platform, in your frame of reference (which is always at rest) the train is at rest relative to your frame of reference. The railroad platform, on the other hand, is moving with respect to your frame of reference. For someone standing on the platform waving goodbye, the railroad platform is, of course, at rest, and it is the train and you that are speeding away – all is relative.
Mathematically, the Special Theory of Relativity describes reference frames as coordinate systems in a four-dimensional spacetime called Minkowski space. Besides three familiar spatial dimensions x, y, z, (or up-down, forward-backward, and right-left):
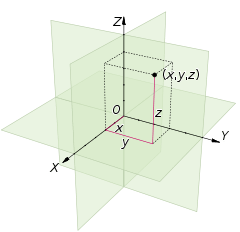
it adds the forth temporal dimension t.
The laws of nature should be invariant with respect to coordinate transformation. This means that no matter what coordinate system you chose, it should not affect the laws of nature – they are the same at every point in space and every moment in time. In mathematics, this is called symmetry.
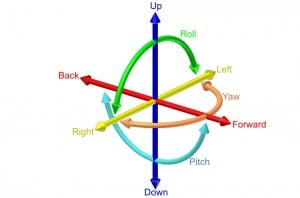One type of symmetry in space is rotational symmetry. If we rotate our coordinate system around an axis, say the z-axis, this should leave something unchanged. That something is a vector in the Minkowski space. Herman Minkowski was Einstein’s math professor in college, who first proposed to unify space and time into a 4-dimensional spacetime continuum, the World, as he called it.
Rotations around an axis of the coordinate system leave the magnitude and the direction of a vector unchanged, or, in the language of mathematics, invariant. Any coordinate transformations in Minkowski space are called Lorentz transformations after Hendrich Antoon Lorentz, Dutch physicist who first mathematically described time dilation and length contraction at high velocities. Because there are three spatial axes around which we can rotate the coordinates, there are three such Lorent rotations.
Hendrik Antoon Lorentz
Another type of symmetry is a Lorentz boost – the transition from one frame of reference to another frame of reference moving with a constant velocity along a straight line. Since such a frame can move with respect to our chosen frame of reference in three different directions, there are three such Lorentz boosts.
All such transformations that leave a vector of the Minkowski space invariant make up the so-called Lorentz group. Because there six types of such transformations – three rotations and three boosts – the Lorentz group has six parameters or six dimensions.
Henri Poincaré
Besides rotations and boosts, there are other coordinate transformations – translations – when we move the whole coordinate system along one of the four axes (in three directions in space and in time). These four translations that leave the magnitude of a vector invariant (although they move the vector to another place) when added to the Lorentz group expand it to what is called Poincaré group. Henri Poincaré was a French mathematician who contributed to the development of special relativity.
Because there are four axes – three spatial and one temporal – there are four additional parameters in the Poincaré group. Together with six parameters of the Lorentz group, the Poincaré group has a total of ten parameters or ten dimensions. Let us summarize these parameters in the following table
Poincaré Group
| Three rotations | Three rotations around the X, Y, Z axes |
| Three boosts | Tree Lorentzian boosts |
| Three translations | Three translations along spatial axes X, Y, Z |
| One translation | One translation along the time axis T |
| Ten | Ten parameters or dimensions |
Alternatively, we can group these parameters as
| Three rotations | Three rotations around the X, Y, Z axes |
| Three boosts | Tree Lorentzian boosts |
| Four translations | Four translations along X, Y, Z, T axes |
| Ten | Ten parameters or dimensions |
Emmy Noether (1882-1935)
The Poincaré group describes all symmetries and, therefore, the geometry of the Minkowski space. Thanks to the famous Noether Theorem formulated by Jewish-German mathematician Amalie Emmy Noether, we now know that every symmetry corresponds to a physical conservation law. For example, the translational symmetry is responsible for the momentum conservation, rotational symmetry is responsible for the conservation of angular momentum, and time-symmetry is responsible for energy conservation. Thus, the Poincaré group not only defines the geometry of relativity but the physics of it as well. It is the foundation of the Theory of Relativity and Quantum Field Theory – the Standard Model. It is indeed the foundation of modern physics.
According to Kabbalah, the physical world we live in is a reflection of higher spiritual worlds that have a similar structure. It is logical to assume, therefore, that the spiritual space and time in the spiritual worlds above have the same geometry as the physical world below. If the physical world is just a reflection of the spiritual realm, we should expect to find the Poincaré group in the spiritual space.
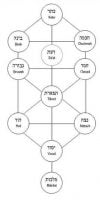The Kabbalah teaches us that the structure of the spiritual worlds is built around ten sephirot. (Few things irk me more than when people compare ten sephirot to ten dimensions in the string theory. It’s a tortured analogy – besides the number ten, they have nothing in common!)
Just the fact that there are ten sephirot and ten parameters of the Poincaré group would not be enough to draw an analogy. But let us look at the structure of the ten sephirot:
Ten Sephirot
| Three Categories of ChaBaD | Three intellects – Chochmah, Bina, Daat |
| Three Primary Emotions – HaGaT | Chesed, Gevurah, Tiferet |
| Three Secondary Emotions | Netzach, Hod, Yesod |
| One Female Principle | Malchut |
| Ten | Ten Sephirot |
Or, alternatively,
| Three Categories of ChaBaD | Three intellects – Chochmah, Bina, Daat |
| Three Primary Emotions – HaGaT | Chesed, Gevurah, Tiferet |
| Four lower sephirot – NeHYM | Netzach, Hod, Yesod, Malchut |
| Ten | Ten Sephirot |
Sometimes, the four lower emanations, Netzach, Hod, Yesod, Malchut, are grouped together. For example, when discussing the differences between Shabbat, Sabbatical year, Shemita, and Jubilee, Yovel, the Arizal says that during Shabbat, four lower sephirot – Netzach, Hod, Yesod, Malchut (NHYM – pronounced Nehim)are elevated together (see Sefer Likutim, Behar). In the language of the Zohar, these for lower sephirot make up the “lower body.”
If you have not yet noticed the similarity, let me now bring ten parameters of the Poincaré group and ten sephirot together:
| Number | Parameters of Poincaré Group | Sephirot |
| Three | Three rotations around the X, Y, Z axes | Three intellects – Chochmah, Bina, Daat (HaBaD) |
| Three | Tree Lorentzian boosts | Chesed, Gevurah, Tiferet (HaGaT) |
| Three | Three translations along spatial axes X, Y, Z | Netzach, Hod, Yesod (NeHY) |
| One | One translation along the time axis T | Malchut |
| Ten | Ten parameters or dimensions | Ten Sephirot |
Alternatively,
| Number | Parameters of Poincaré Group | Sephirot |
| Three | Three rotations around the X, Y, Z axes | Three intellects – Chochmah, Bina, Daat |
| Three | Tree Lorentzian boosts | Chesed, Gevurah, Tiferet |
| Four | Four translations along spatial axes X, Y, Z, T | Netzach, Hod, Yesod, Malchut |
| Ten | Ten parameters or dimensions | Ten Sephirot |
We see that both the Poincaré Group and the Ten Sephirot can be presented as three triads plus the tenth element, which in the Poincaré Group is a translation in time and in sephirot is Malchut. The Kabbalah teaches that time comes from Malchut (of the world of Emanation – Atzilut). Alternatively, both constructs may be presented as two triads and a quartet – four translations in the Poincaré Group corresponding to four lower sephirot that move (translate) together in tandem on Shabbat. The first three sephirot, Chochmah, Bina, and Daat (ChaBaD) are parallel three rotations around axes X, Y, and Z. The second triad of sephirot, Chesed, Gevurah, and Tiferet (ChaGaT) are parallel three Lorentz boosts. And the four lower sephirot, Netzach, Hod, Yesod, and Malchut (NeHYM) are parallel four translations in Minkowski space. Thus, ten sephirot can be viewed as ten parameters (or dimensions) of Poincaré Group. It all now fits together.
These uncanny structural similarities suggest that indeed, just as in the physical space Poincaré group define the geometry, in the spiritual space, ten sephirot define ten parameters (or dimensions) and the structure of the Poincaré group. The Jewish physics indeed!
It’s difficult to say whether it’s amazing or ridiculous that, together with this totally baseless fantasy, the author becomes angry by the equally baseless comparison of the sephirot to the ten dimensions of string theory.
Thanks for your comment. With all due respect, the basis for the analogy was explained at length. If you disagree with the analysis, I’d love to hear why. However, I don’t it’s fair to call the comparison baseless without offering a specific critique of the arguments on which the analysis is based.
I would add to the previous comment by Avinoam Mann, that the comparison is (almost) as baseless as the comparison to string theory, because other than the similar grouping of three 3’s plus one, or two 3’s plus 4, no conceptual similarity between these two systems is offered, which would perhaps have given some credence to the imaginative comparison. What, for example, would be the conceptual connection between the three rotations around the X,Y,Z axes and the three upper sephirot (Intellects, or Mochin, in Kabbalistic terminology) – Chochma, Bina and Daat. In the physical world no axis has any hierarchical advantage over the other two (everything’s relative, right?) Not so in Kabbala. Chochma (while not apparent in the traditional diagram) is always considered a higher sephira than Bina, and likewise Bina wrt Daat. Also, Daat is considered as a resolution, or synthesis, of the two opposing sephirot of Chochma and Bina. A somewhat similar relationship also exists between the next two sets of three sephirot. No such relationships exist (as far as I know) within any of the sets of physical parameters.
Another point of contention: As I’m sure the author knows, there are several other ways of dividing up the ten sephirot, such as: GaR (Gimil Rishonim = the first 3 sephirot) and ZaT (Zion Tachtonim = the 7 lower sephirot), or Keter, Choma and Bina as the first 3, instead of Chochma, Bina and Daat (Keter does, in fact, appear in the diagram, but, I suppose to keep things simple, was not mentioned.) Is there, in fact, a parallel set up of 3 vs 7 physical parameters?
So, again, unless one can propose, or better, quote some authoritative reference for, the conceptual parallels between these two systems, the comparison remains nothing more than a superficial similarity in structure.
Thank you very much for your thoughtful comment. Unlike the comment of Avinoam Mann which offered no argumentation and, therefore, suffered from the very weakness it accused me of – baselessness – your comments are very much to the point.
You raise very valid questions which I struggled with myself. So here are some of my half-baked thoughts on this.
A conceptual similarity is not the subject of inquiry in structural analysis, which is what this is. Quite to the contrary, in structural analysis, we look for relative relations between objects (or subjects in a literary analysis) taken out of context. A useful tool for that is to rename all objects (or subjects) with abstract labels such as A, B, C… or X, Y, Z or whatever, not be burdened with the contextual weight the real names bring to bear. If you forget, arguendo, that we are talking about sephirot, and relabel them with abstract labels, you would not be facing many of the questions you are raising.
Firstly, allow me to addres if it is appropriate to analogize sephirot to any geometrical structure of a conceptual (or physical) space. I would submit to you that Sefer Yetzira did just that. As we discussed in a number of my older posts (On the Nature of Time and the Age of the Universe, The Fifth Force, The Fifth Force – Epilog, Tumah and Taharah), Sefer Yetzirah, the oldest surviving book of Kabbalah, describes our world as a five-dimensional universe: A depth of beginning, a depth of end; a depth of good, a depth of evil; a depth of above, a depth of below; a depth of east, a depth of west; a depth of north, a depth of south. (Sefer Yetzirah 1:5). This structure is easily mapped onto seven lower sephirot (see my posts referenced above).
As Rabbi Kaplan explained very well in his book The Inner Space, a spiritual space is a conceptual space where each point represents a concept. It is easier to define a metric on such a space, as the conceptual closeness of two points representing the two different concepts. The more similar the concepts are, the closer the two points are in this space. If concept A occupies the point PA, and concept B occupies the point PB, we can say, if A=B, then PA = PB. If, on the other hand, A is the negation of B, points PA and PB are infinitely far from each other, or are on the opposite “poles” of this space. Perhaps, rotations in such a space could be viewed as a reorientation of one’s point of view. Choosing a specific coordinate system is, in fact, mathematical formalization of choosing a “point of view.” Rotating such coordinate system around one of the axes is equivalent to reorienting one’s point of view or one’s “angle of view.” Indeed, sephirot, as vessels for the infinite light of Ein Sof, are analogized in Kabbalah to color glasses through which we related to the Light. In other words, they offer different colors or “angles” of viewing reality. In my analogy, mathematically speaking, the first three sephirot – Keter, Chokhmah, and Binah; or Chokhmah, Binah, and Daat – can be viewed, perhaps, as parameters of rotation of this conceptual reorientation.
You raise a fair point about the hierarchical organization of sephirot which is absent in geometry. Please note, however, that such hierarchical organization is only found in one of three main representations of sephirot – the anthropomorphic representation called Ish – Man. In the scheme of Igulim, Circles, the sephirot are envisioned as concentric circles with no right, left, or middle columns. Similarly in 5+5 representation, such as found on fingers of our hands or feet, or the Ten Commandments on the Luchot arranged (in most opinions) as five and five, the only symmetry is the mirror symmetry between two groups of sephirot, which are no longer hierarchical.
The relationship between GaR and ZaT is easy to envision too. In the physical world, the seven midot (lower sephirot also referred to as ZaT) represents the cartesian coordinat system with six midot (also referred to as partzuf Zeer Anpin, Z”A) representing the opposite direction of each coordinate axis (“the depth of up and the depth of down”), with Malchut (Nukva d’Z”A) representing the center of coordinate system. This is what is acted out during the holiday of Sikkot when we wave arba minim – naanuim in all six directions every time bringing lulav back our heard. The man in the center wich his three intellectual faculties of Chokhmah, Binah, and Daat represent the first three eponymous sephirot. I’ve written about it my post “Menorah.”
Once again, thank you for your very thoughtful questions that compelled me to explain these issues in greater detail.